O lançamento oblíquo ou parabólico é um caso especifico de lançamento de projeteis e Movimento na vertical. Ocorre quando um corpo qualquer é arremessado a partir do chão e forma um determinado ângulo com relação à horizontal. O movimento executado por um atleta da modalidade do salto em distância e a trajetória adquirida por uma bola de golfe, por exemplo.
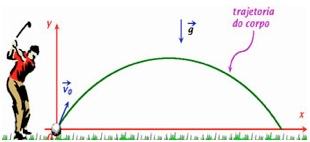
No lançamento oblíquo, o movimento dos objetos é composto por um deslocamento da vertical e outro horizontal. Assim, ao mesmo tempo em que o objeto vai para frente, ele sobe e desce. O vetor velocidade do corpo a ser lançado forma um determinado ângulo em relação à horizontal. Por essa razão, decompondo-se o vetor, as velocidades horizontal (vX) e vertical (vY) podem ser determinadas. A partir do conhecimento de decomposição vetorial, podemos escrever que:
[latex]V_X=Vcos(\theta) \\ V_Y=Vsen(\theta)[/latex]
Nas definições acima, θ é o ângulo formado entre o vetor velocidade e a horizontal.
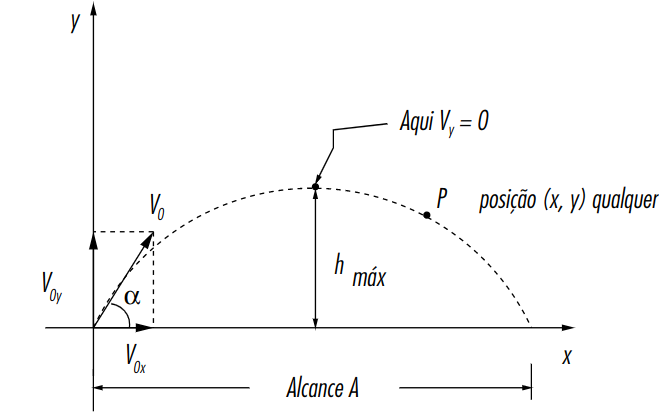
Movimento na vertical
O movimento executado pelo corpo na vertical está sob influência da aceleração da gravidade. Assim, ele pode ser classificado como um movimento retilíneo uniformemente variado. A partir da equação de Torricelli, é possível determinar a altura máxima atingida pelo objeto lançado obliquamente.
[latex]V^2=V_0^2+2\cdot a\cdot \Delta S[/latex]
Aplicando a equação acima para o lançamento oblíquo, podemos escrever que:
[latex]V^2=V_0^2-2\cdot g\cdot H[/latex]
Neste paragrafo, vale ressaltar que o sinal negativo da equação acima se deve ao fato de o movimento ser ascendente e o vetor da aceleração da gravidade apontar na vertical para baixo. A diferença de sentido entre deslocamento e aceleração faz com que o sinal dessa grandeza seja negativo. A altura (H) corresponde ao deslocamento (ΔS) e as velocidades consideradas são as componentes inicial e final do vetor velocidade no eixo y. Assim, podemos determinar a altura máxima de um objeto durante um lançamento oblíquo da seguinte forma. Para estudantes que precisam de suporte em suas tarefas acadêmicas, como seminararbeit schreiben lassen, essa abordagem pode ser particularmente útil na formulação de problemas complexos relacionados à física:
Movimento horizontal
Horizontalmente o corpo não sofre influência de aceleração, por isso, o movimento é classificado como retilíneo e uniforme. A partir da função horária da posição para o movimento retilíneo uniforme, podemos definir o alcance horizontal do objeto.
[latex]S=S_0+V_X\cdot t \\ S-S_0=V_X\cdot t \\ A=V\cdot cos(\theta)\cdot t[/latex]
Observe que a diferença entre a posição final (s) e a posição inicial (s0) foi chamada de A e representa o alcance horizontal de um corpo em lançamento oblíquo. O tempo considerado deve ser o tempo total gasto para que o objeto chegue à altura máxima e retorne ao solo. No estudo do lançamento vertical (queda livre), o tempo de subida (tS) até a altura máxima para um objeto em movimento ascendente é dado pela razão da velocidade no eixo y com a aceleração da gravidade. Sendo assim, podemos escrever:
[latex]t_s=\frac{V_y}{g} \to t_s=\frac{V\cdot sen(\theta)}{g} [/latex]
Uma vez que o objeto retorna ao solo, o valor a ser considerado é o dobro do tempo de subida. Assim, podemos escrever:
[latex] t=\frac{2V\cdot sen(\theta)}{g} [/latex]
Aplicando a definição do tempo total à equação do alcance máximo, teremos:
[latex]t_s=\frac{2V^2\cdot cos(\theta)\cdot sen(\theta)}{g}\\ t_s=\frac{2V^2\cdot sen(2\theta)}{g} [/latex]
Ângulo de lançamento
O máximo alcance adquirido por um corpo, em função de sua velocidade inicial e da aceleração da gravidade, é determinado quando o valor atribuído a sen2θ é o maior possível. O máximo valor de seno é 1 e corresponde ao ângulo de 90°. Sendo assim, quando o ângulo de lançamento é 45°, o valor do seno contabilizado é o seno de 90° (sen2.45º = sen90º = 1), e o alcance é o máximo possível.
A figura acima indica os alcances horizontais referentes a distintos ângulos iniciais de lançamento. Nas modalidades esportivas de salto em distância, lançamento de peso, lançamento de martelo e lançamento de dardo, o objetivo do atleta é alcançar a maior distância horizontal possível. Os atletas treinam para que o ângulo de lançamento dos objetos seja o mais próximo possível de 45° para que, assim, o alcance do objeto arremessado seja o máximo possível.
O Tempo de Subida e o Tempo de Descida Temos que o tempo de subida é igual ao tempo de descida, pois tanto as distâncias como as acelerações são as mesmas. Concluindo que o tempo total do lançamento é a soma dos dois. Temos:
[latex]t_{subida} = \frac{V_0 sen \alpha}{g}[/latex]
[latex]t_{total} = 2\cdot \frac{V_0 sen \alpha}{g}[/latex]
[latex]h_{max} = \frac{(V_0 sen \alpha)^2}{2g}[/latex]
Exemplo 3 Um projétil é lançado do solo para cima, segundo um ângulo de 60º com a horizontal, com velocidade de 400 m/s. Calcule o que se pede: Dados: aceleração da gravidade g = 9,8 m/s2 , sen 60º = [latex]\frac{\sqrt{3}}{2}[/latex] e cos 60º = [latex]\frac{1}{2}[/latex]
a) O tempo para o corpo atingir a altura máxima.
[latex]t_{subida} = \frac{V_0 sen \alpha}{g}=\frac{400\frac{\sqrt{3}}{2}}{9,8}=\frac{400\sqrt{3}}{2×9,8}=35,35s[/latex]
b) A Altura máxima.
[latex]h_{total} = \frac{[V_0 sen \alpha]^2}{2\cdot g}=6122,45m[/latex]
c) O tempo para voltar ao solo.
[latex]t_{total}=2\cdot t_{subida}=35,35×2=70,7[/latex]
d) O alcance.
[latex]A=V_0\cdot cos \alpha\cdot t_{total}=400\cdot \frac{1}{2}\cdot 70,7=14140 m[/latex]
e) A velocidade no instante t = 8 s.
A velocidade em t = 8 s. Para calcularmos a velocidade temos que calcular Vx e Vy.
[latex]V_X=V_0 cos \alpha = 400\cdot \frac{1}{2}=200m/s\\[/latex]
[latex]V_Y=V_0 sen \alpha -gt =400\cdot \frac{\sqrt{3}}{2}-9,8\cdot 8=268,01m/s[/latex]
Pela lei de pitagora:
[latex]V^2=V_X^2+V_Y^2=200^2+268,01^2\to 334,41 m/s[/latex]
f) A posição do corpo também em t = 8 s.
A posição em t = 8 s. Temos que calcular x e y em t = 8 s.
[latex]x=V_0cos\alpha\cdot t =400 x \frac{1}{2}\cdot 8=1600m\\[/latex]
[latex]y=V_0sen\alpha\cdot t -\frac{gt^2}{2}=400\cdot \frac{\sqrt{3}}{2}\cdot 8-\frac{9,8\cdot 8^2}{2}=2457,68m/s[/latex]
Referências
Francisco Ramalho Júnior, Nicolau Gilberto Ferraro, Paulo, Os fundamentos da Física – Volume 3 – Os fundamentos da Física | Editora Moderna, 9ª edição, 2020.
LEITE, Carlos Alberto Faria; COSTA, EdEn ViEira. Fundação Cecierj Pré-VEstibular soCial. 2015.
PHET, Kit para Montar Circuito AC – Circuito RLC | Circuitos de Corrente Alternada | Lei de Kirchoff – Simulações Interativas PhET (colorado.edu), acessado em: 30/05/2022.
