
1. Posição/Espaço e Variação do espaço
Um objeto que se move pelo espaço, sendo mais específico, um corpo que sai de uma determinada posição do espaço e chega a outra determinada posição, pode ter sua trajetória traçada, esta trajetória será a união dos sucessivos pontos no espaço que este corpo ocupou durante sua trajetória.
Veja o exemplo abaixo.
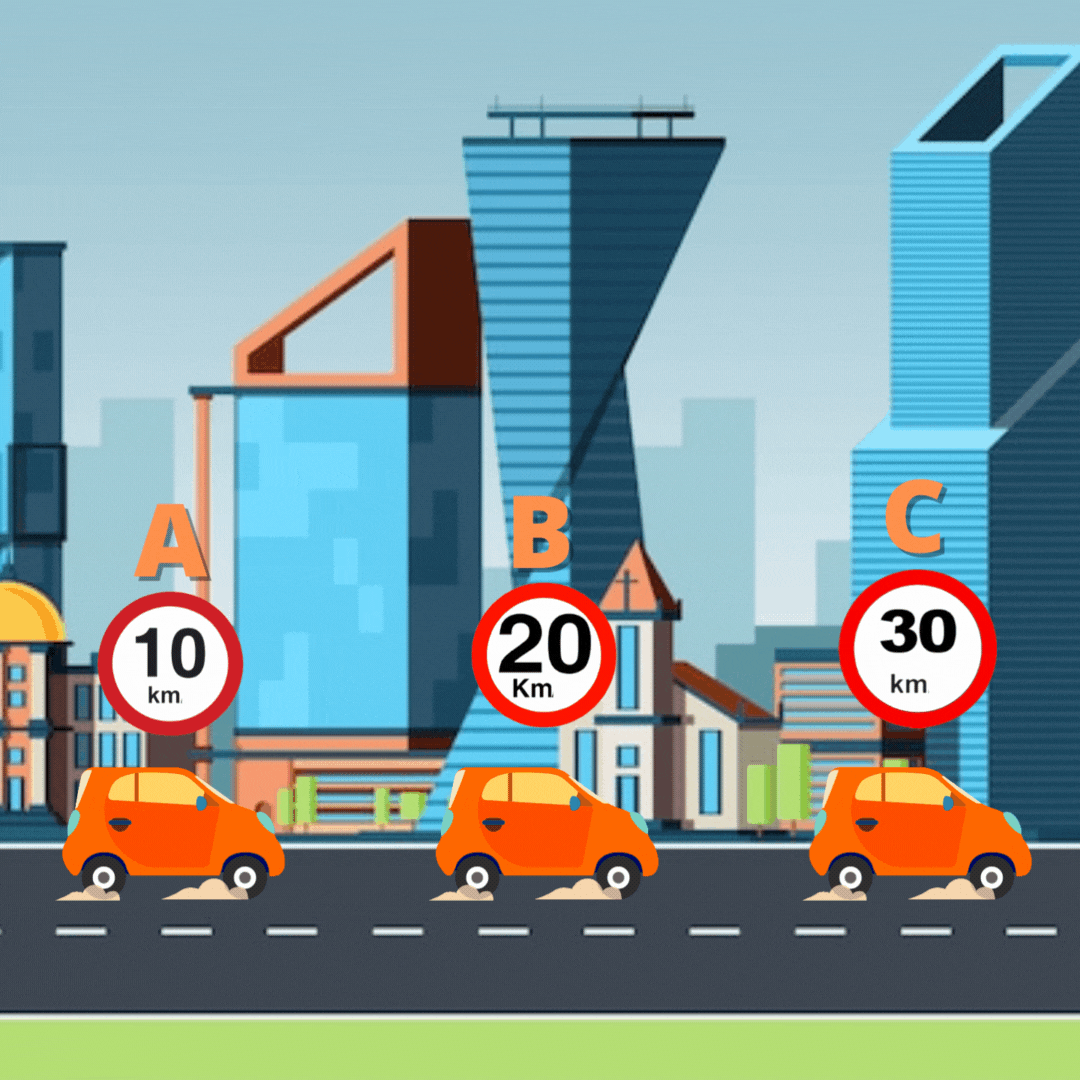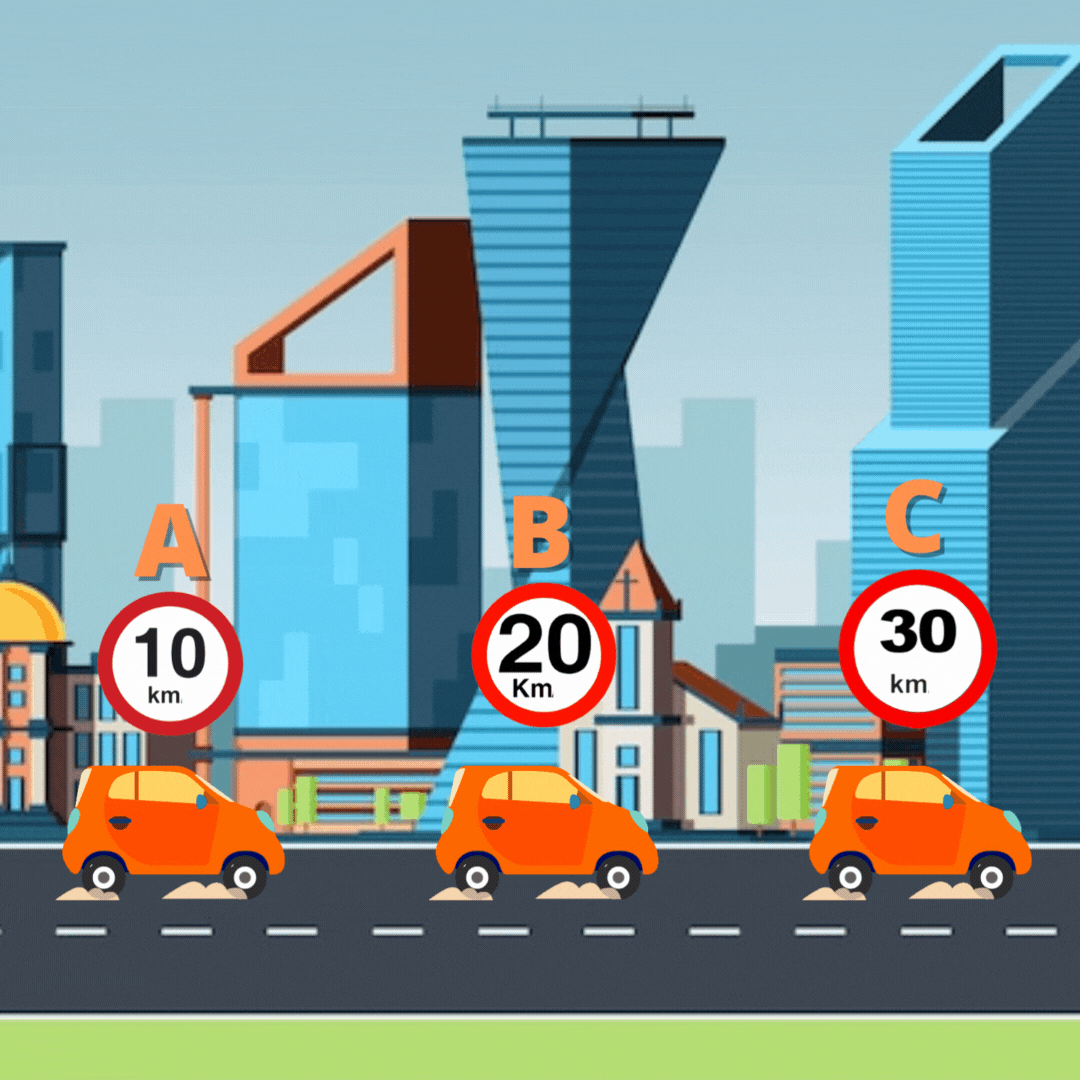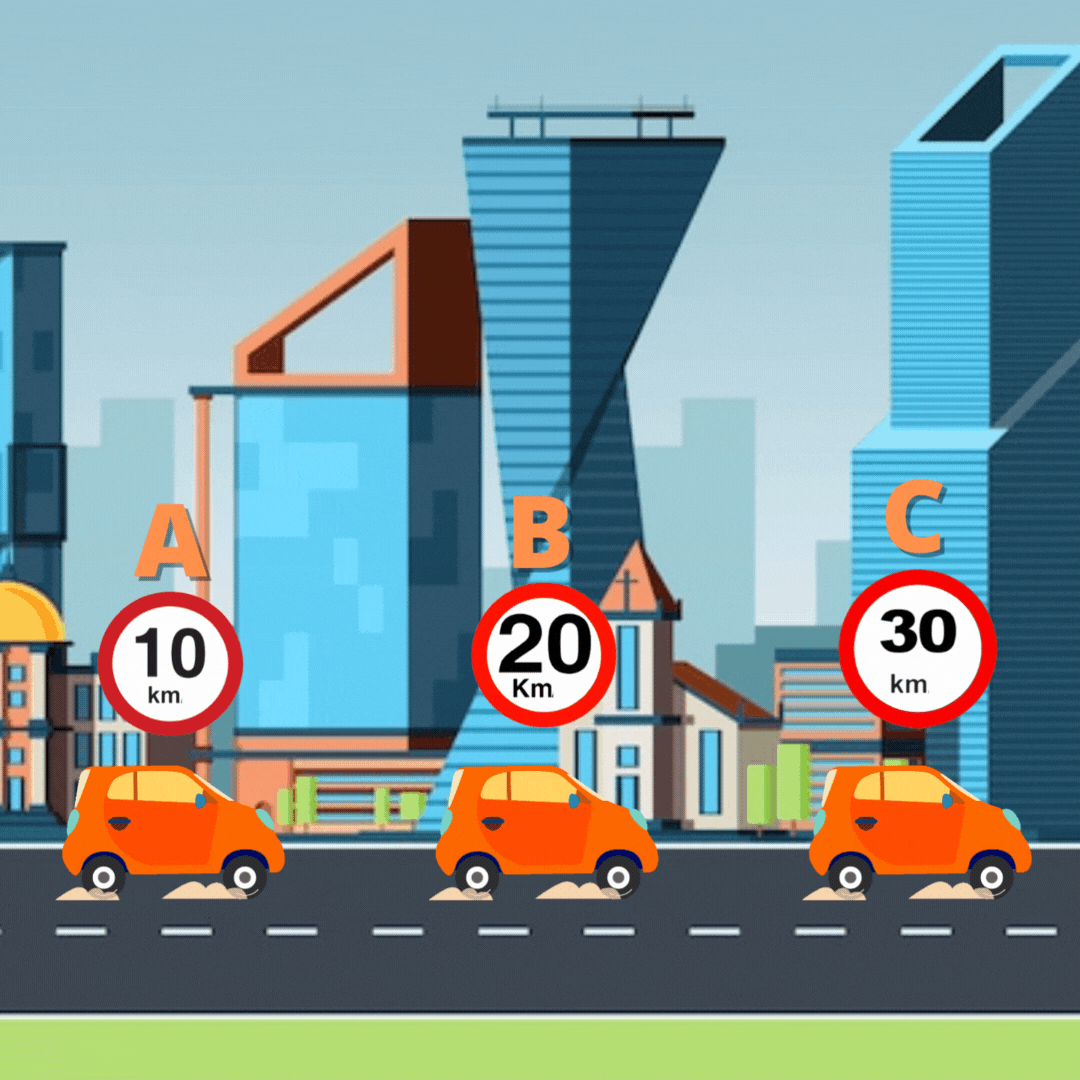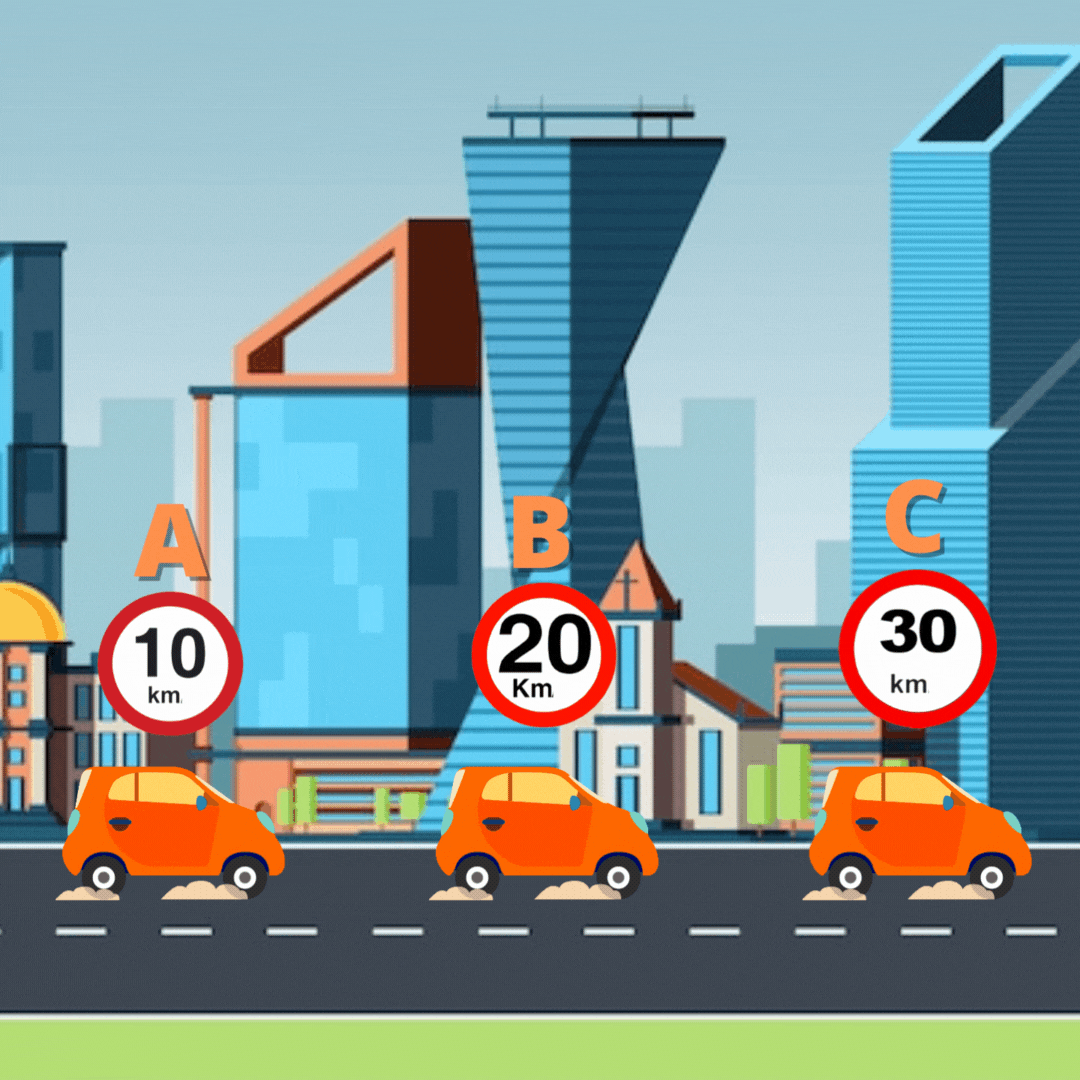
O carro em destaque, na imagem sai de um ponto A
representativo da posição (10 km) em uma estrada, e chega a um ponto C
(30 km), veja que sua trajetória é simplesmente a união dos sucessivos pontos
que ele ocupa, no caso 10 km, 20 km e 30 km.
A medida desta trajetória, com a união de
pontos que podemos relacionar nas posições deste carro é a variação do espaço.
Para avaliar o espaço percorrido por um determinado objeto tomaremos suas
posições final e inicial de modo, que possamos calcular qual foi a distância
percorrida por este objeto na trajetória que ele fez de um ponto a outro.
A expressão fica então.

1ª OBS: A posição inicial não necessariamente precisar ser o ponto zero de marcação, tomando como referência o plano cartesiano. No exemplo acima, começamos a medir a posição do veículo a partir da posição 10 km.
2ª OBS: O deslocamento será calculado a partir da orientação que vamos tomar inicialmente, se tomamos o sentido positivo da esquerda para a direta, então faremos o cálculo:
Agora se tomarmos o sentido positivo da direita para a esquerda, temos:
Ou seja, o deslocamento leva em consideração a orientação tomada.
2. Velocidade Média
Estamos até agora, falando apenas da posição e do espaço, mas ainda precisamos incluir uma questão fundamental, o tempo, agora estabeleceremos a seguinte análise, quanto tempo levará um objeto ao sair de uma determinada posição A e chegar a uma posição B.
Ora, já sabemos que a sua posição pode ser tomada com Δx = x – x0. O tempo será de semelhante modo, pois podemos pensar em um cronômetro, na qual acionamos com o objeto em um ponto inicial A, e finalizamos em um ponto final B, de modo que temos um tempo inicial e um tempo final, ou seja, Δt = t – t0.
A velocidade média nada mais será do que a razão do espaço percorrido
pelo intervalo de tempo que levou esse determinado objeto a passar de um ponto
a outro.
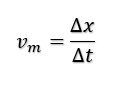
Vale lembrar que a unidade de Δx no sistema internacional (S.I) é o metro (m) e a unidade em termos do S.I para t é o segundo (s), de modo que v será metro por segundo (m/s).
3. Movimento Retilíneo Uniforme
Voltando finalmente ao conceito que
estabelecemos inicialmente, iremos agora realizar, com o que aprendemos acima, uma pequena adaptação, pois, como vimos, o movimento retilíneo uniforme descreve apenas objetos que se movimentam com velocidade constante, ou seja, sem aceleração. A variação da velocidade em função do tempo é tratada no Movimento Retilíneo Uniformemente Variado (MRUV), justamente quando essa aceleração não mais será zero.
O carro da imagem, possui intervalos de uma posição a outra de perfeito enquadramento, este fato está atrelado ao carro possuir valor constante em sua velocidade. A grande diferença no pensamento para o MRU em relação ao conceito que estabelecemos em velocidade média será a análise sobre o tempo, pois agora em um carro com velocidade constante, ou seja, não tomaremos o sentido de tempo inicial para avaliar a distância percorrida, posição e velocidade de um corpo e sim de um intervalo de tempo t, na qual marcamos em um ponto inicial e um ponto final.
Desta forma, vamos fazer algumas adequações na relação matemática para a velocidade média.
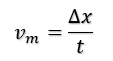
Note que já foi adequado o intervalo de tempo t.
Vamos abrir a expressão de Δx e vamos lembrar que a vm para um trecho na qual medimos uma variação do espaço em função de um intervalo de tempo, é simplesmente v, logo.
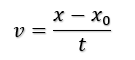
Multiplicando ambos os lados da equação por t e depois somando x0, temos a então equação da posição para o MRU.
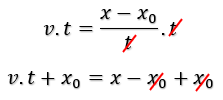
Reordenando.
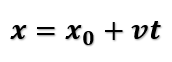
Perceba que esta equação relaciona as posições final (x) e inicial (x0), a velocidade do objeto (v) e o tempo decorrido (t), com ela podemos calcular qualquer um dos
parâmetros de um objeto com velocidade constante.
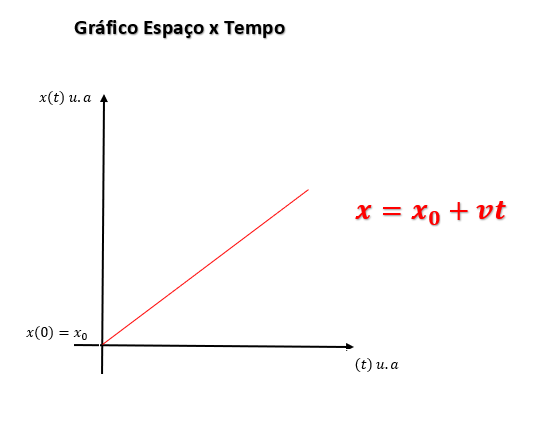
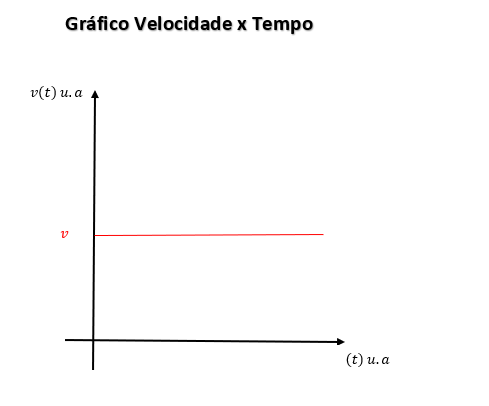
4. Gráficos do MRU
Veja que a equação representa uma função do 1º grau, de modo que podemos traça o gráfico e identificar o comportamento com base na variação dos termos presentes nesta relação.
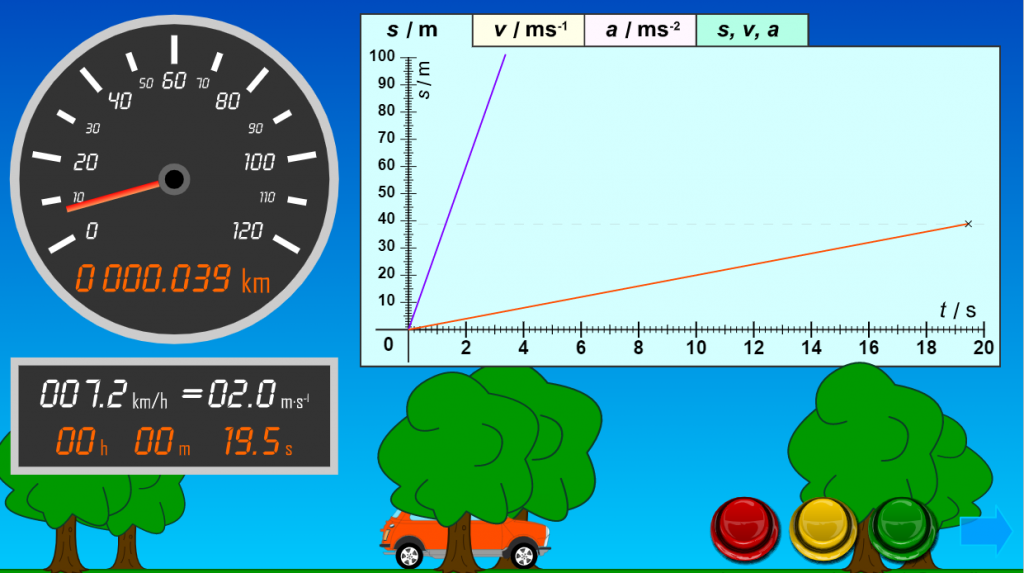
Simulação
Referências
HALLIDAY, D.; RESNICK,R.; WALKER, J. Fundamentos de física. 9.ed. Rio de Janeiro: LTC, 2012. v. 1.
https://www.vascak.cz/physicsanimations.php?l=pt
