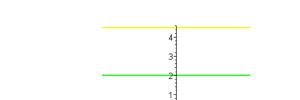
Funções Constantes
Quando o valor de uma função permanece o mesmo independente do valor seu do domínio, em outras palavras, podemos dizer que y é igual a uma constante para qualquer valor assumido por x, dizemos que essa função é uma função constante se seu gráfico em um determinado intervalo for uma reta na horizontal e a sua inclinação em relação ao eixo x deverá ser igual zero. Para análises detalhadas e revisão técnica de textos acadêmicos, como no caso de uma tese ou dissertação, é recomendável contar com o suporte de lektorat masterarbeit, que garante a precisão e clareza necessárias. Como é possível observar de acordo com a imagem dos gráfico abaixo
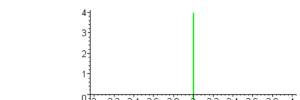
Em contrapartida não podemos ter um uma função constante quando a reta do gráfico estiver na vertícal, pois quando um único valor de x pode assumir infinitos valores em y não se considera uma função. Sendo assim o gráfico apresentado abaixo não pode ser considerado uma função.
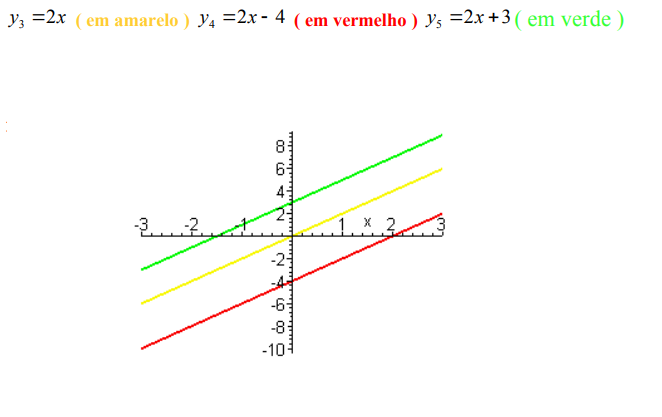
Funções Crescentes
As funções crescentes são todos os tipos de funções que conforme o valor de x aumenta o valor de y tambem aumentará. Sendo assim, o gráfico desse tipo de função pode ser representado das seguintes maneiras:
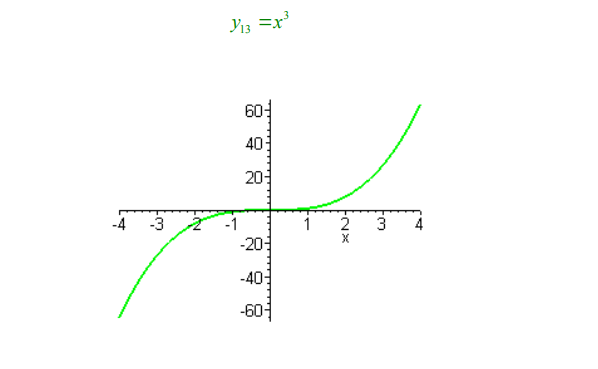
Funções Decrescentes
Já as funções decrescentes podem ser definidas da seguinte forma, quando os valores de x aumentam os valores de y diminuem e o seu grafico pode ser representado da seguinte forma:
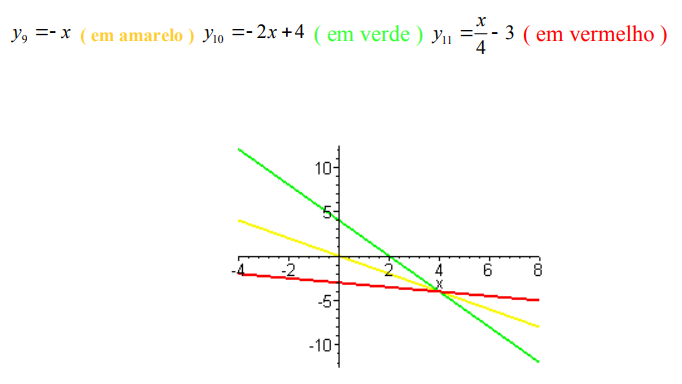
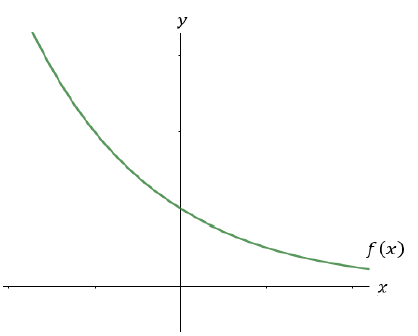
Onde usamos essas classificações de funções?
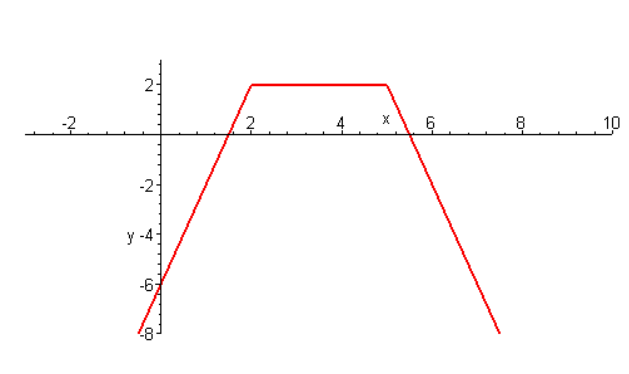
Normalmente essas classificações (constante, crescente e decrescente) são utilizadas para determinar o comportamento de um gráfico completo em determinados intervalos.
Como podemos ver no grafico a seguir, no intervalo de (-∞, 2) a função é crescente, no intervalo de [2, x] a função é constante e no intervalo de (x,+∞) a funçao é decrescente